Download this post (PDF)

Quantifying and estimating project and investment results are very important for financial planning, investment comparison and decision making purposes. However, business is always conducted in an uncertain environment while financial planning is commonly done using single-value revenue and cost-side estimates, which managers assess using rules of thumb. While fast to come up with, these methods factor in risks and upside potential poorly. This is a typical issue in project businesses such as manufacturing of industrial goods, new business building, and businesses where market values of raw materials and/or end-products tend to be volatile, like mining or petrochemical industries. Often the numbers are also not thought through before putting them into the budget. Accuracy and reliability of the forecasts can be sharpened simply by adding the worst and best case estimates and applying some mathematical methods.

As discussed in our previous article on stochastic budgeting, forecasting revenue and costs is too often based on only one single-point estimate for each reporting unit. Such rough estimates vary according to who is making the estimates and are often subjective. Managers might discount uncertainties and drive ambition level in budgets by using simple rules of thumb such as percentage level increases or decreases in the estimates. In our previous article, we discussed project likelihood estimates as a solution to the problem. In this article, we present an approach where the best, base and the worst case scenarios are used to improve the estimates.

Towards better budgeting – recognizing uncertainty

There are various ways to address uncertainty and reduce subjectivity in financial planning. One can estimate multiple points for each value and their associated probabilities, and then apply mathematical methods to assess the most probable value and confidence levels. Calculating the estimate from multiple points increases objectivity of the resulting budget line, although the subjectivity of the data points themselves remains. Adding data points still makes it harder to manipulate the end-result and forces to think and argue why the value and probability should be as presented. A simple method often utilized to increase objectivity is collecting inputs for the same items from more than one person, although the efficient use of time and amount of real expertise available for giving inputs should be considered. The problem with these approaches is that assessing probabilities in a business environment is inherently inaccurate and often no more than educated guessing.

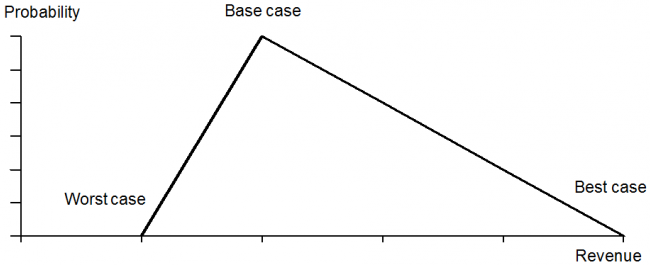
The method we propose instead is creating a range for each value by defining the best, worst and base case (usually representing the mode value of the probability distribution) scenarios for each line item in the budget. Figure 1 shows an example of a revenue line item such as a revenue forecast of a project. This very intuitive approach has many benefits. With the three cases approach, all the user of the model needs to do is to give values for each scenario without the need to consider probabilities, as the model inherently assumes a probability distribution. Also, the approach makes it is easier to explain and justify the budget line, as it is calculated based on scenarios that are easy to understand. For example, a manager who is not “satisfied” with the budgetary values achieved this way is forced to think and discuss the reasons for the different scenarios. Discussion about low and high scenarios facilitates the conversation about market uncertainties and improves the understanding of risks and drivers of the market.

Figure 1. The three scenarios approach for a revenue line item

As a way to apply the three scenarios approach in budgeting, managers can choose to use the best case scenario as the target to inspire the organization, whereas for treasury and risk management purposes the more conservative figures provided by the model should be used. Models are at their best when opinions and politics matter very little in the end result, whereas when inspiring organization to the best results, choosing and communicating too low targets and relying only on models can easily be counterproductive (see for example Rosenzweig 2014).

In addition to the ease of collecting inputs, the ability of the model to yield a complete probabilistic budget to help with risk management and more accurate planning is a major part of its value. It is able to answer questions such as:

• What is the most probable P&L?
• What is the probability that we break even in a given period?
• What is the 25%…75% confidence interval for our profit in a given period?

Knowing the confidence levels in addition to the most probably values is important for example in cash management, where it is very beneficial to have an understanding also on the minimum cash flows. Also, when choosing which project to invest in, it is beneficial to understand the potential upside and downside, not just the expected value. To achieve this, as mentioned earlier, the model provides an intuitive way to assess the probability distributions that does not require advanced mathematics.

Relating the model to reality

It is always a challenge to balance scientific rigor with what is practical from a business perspective. A statistical distribution used to model a variable should always be related to the observed distribution. In statistics, the normal distribution or Student’s t-distribution are often the chosen ways to describe the world because of their mathematical properties and almost magical ability to describe different phenomena found in nature. In business, it is often the case that nothing is known of the statistical properties of for example the revenue of a project for the coming years. Furthermore, the upside potential skews the distribution while the worst case tail of revenue ends at 0 – a clear deviation from the normal and t- distributions limiting their applicability. The usability of the approach should also be considered: it would not be reasonable to demand a sales person to fill in estimated skewness, kurtosis and standard deviation of his sales estimate for the upcoming year.

While one of the benefits of the three-point estimate approach is that it can be utilized with virtually any distribution, we advocate a very simple triangular distribution which inherently bears many useful properties from a budgeting perspective. Despite all the virtues and mathematical properties that using more complex distributions might bring in, the trade-off is intuitiveness and understandability of the model which matter much more in the business environment. The triangular distribution is a probability distribution that decreases linearly from the mode value to the minimum and maximum values so that the total probability reaches 1 and can be automatically calculated when the distance between the three points is known.

When continuous triangular distribution is linked to the three point scenarios, the worst case, best case and the most likely to occur (modal) values are respectively the left corner, right corner and the “peak” of the “triangle” that the triangular distribution forms, as can be seen in Figure 2. Because the triangle is formed with so few data points, it is also called a lack of knowledge distribution. The lack of knowledge name suits also many business applications where exact data on the variables is not available or would be too costly to collect.

Figure 2. Example triangular distribution of revenue

Assessing the uncertainty with simulations

Even though an analytical solution might be easy to find for example for the most likely value of one variable with worst, base, and best case scenarios and triangular distribution, assessing the most likely outcome of a system of multiple uncertain variables dependent or independent of each other can soon become very difficult at least in a closed form. For example, the EBIT of a company or P&L responsible unit usually comprises of numerous projects and line items which are affected both from the revenue and the cost side by numerous sources of uncertainty, with differing amount of dependency between the line items. Often for example the cost of goods sold follows the revenue quite closely while the operating expenses might not be very variable.

The distribution and confidence levels of the outcome of a complex system are most easily assessed by using simulation methods such as Monte Carlo. For example, a triangular distribution of revenue shown in Figure 2 would be simulated so that a random number is generated multiple times and each time mapped to the triangle shown. In the end, the results are aggregated together and analyses are conducted to find the most probable outcome. It is of course very easy to find an analytical solution to the most probable revenue in the case depicted in figure 2, but when complexity is increased, finding closed form solution becomes more and more difficult. Using simulations becomes very useful in understanding budgets of multiple line items with independent variables, because in those situations the most probable EBIT or cash flow outcome is not the sum of the most probable individual line items.

Monte Carlo methods are based on repeating “the experiment” multiple times within a pre-determined domain and then aggregating the results of the multiple experiments. To make the simulations reliable, they need to be repeated a certain number of times that depends on the used distribution, estimated standard deviation and the level of acceptable error. Usually a minimum of 1000 simulation rounds, and preferably one magnitude more, should be made regardless of the system to achieve acceptably small error levels for the simulation. On the other hand, computational limits need to be considered when using a very large amount of simulations in a complex system.

Increasing the understanding of market drivers through objective discussion

When doing budgeting in practice, it might at first sound heavy or unreliable to implement sophisticated mathematical methods. However, besides improved objectivity, using stochastic budgeting might actually end up saving a lot of time and money as stakeholders do not need to arm-wrestle on the numbers, in which case objectivity is easily lost completely. Results might actually be improved as all parties can bring their views on the worst, base and best case to the table and simply calculate the most probable outcome. If the outcome is somehow different than was expected by the “gut feeling”, then clear benefits can be achieved by discussing and analyzing whether the base line, worst and best cases are reasonable and a better understanding of the related risks, opportunities and market drivers is reached.

Using the method outlined in this article, the individual estimates can then be built into a most probable P&L budget for the project or business unit and confidence intervals of given probabilities can be easily calculated. Still, managers should always remember that any model is only as good as its ability to describe the real world, which makes it imperative to always follow-up the forecasts against actuals, and re-iterate the model and the assumptions should there be major differences between the estimates and the realized figures.
__________
References:

Rosenzweig, P. (2014) The benefits – and limits – of decision models, McKinsey Quarterly February 2014